人智学を理解するための射影幾何学入門 by たわふ
森章吾さんによる「人智学を理解するための射影幾何学入門」を受講してきました。
1日目は雨降りの中、2日目は吹雪の中、ひびきの村へ行って来ました(すごい両極端な天気)。
まず、空間をイメージする力を育てる練習。
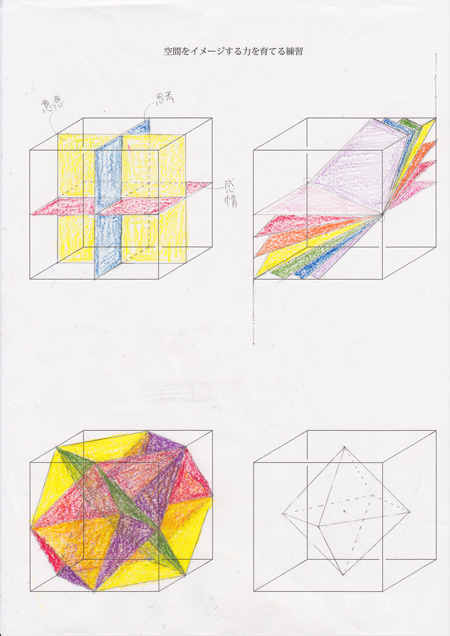
左上は、正六面体を3方向に区切る仕切りを入れた場合、見えるところと見えないところを書き分けて書く。現代科学的には、上下・左右・前後はどれも均一な空間だが、人間からみた感覚で、思考・感情・意思がどこに対応するか?天秤は裁判所のマークとして使われていることからも判断や思考は左右、気分が落ち込むとか気分が上向きと言われるように、感情は上下、後ろ向きな態度という言葉からも、前後が意思と分かる。それに対応する色に、好きな色で塗り分けた。普通に考えたら思考が青で感情が黄色で意思が赤になるのかな?まあでも、なんとなく感情が黄色っていうのが腑に落ちなかったので赤にしてしまった。
右上は、正六面体を斜めに切った場合の切り口の形を1cm間隔で書いたもの。そして色分けしたもの。
左下は、正六面体に斜めの切り口が正六角形になるのは何個あるか?すべてを書き込んだ場合どんな風に見えるかをあわらしたもの。
右下は、正六面体の中の面の中心を頂点とする図形、正八面体を書いたもの。正六面体と正八面体は、すべての面を頂点(点)に、すべての頂点(点)を面に変換する関係で、裏返しの関係。
射影幾何学は、一般的な幾何学に無限遠点を付加することで例外をなくすことができる。たとえば「平面上の2つの直線は1点で交わる」が、平行な直線であれば一般的には交点はない。だが無限遠点が存在することで、平行でも無限遠点という1点で交わることができ、「平面上の2つの直線は1点で交わる」ということがすべての直線で成り立つことになる。

遠近法とはどうゆうものか?物質空間を絵画(平面)に取り込んだ。無限遠点を書き込んだ(つかまえた)。消失点が無限遠点。鑑賞者の立つ位置が決まってしまう。セザンヌの絵は遠近法的に見ると歪んでいるそうだ。でもそれはわざとしていることで、絵画空間を創りだしている。緊張感をだしているとのこと。
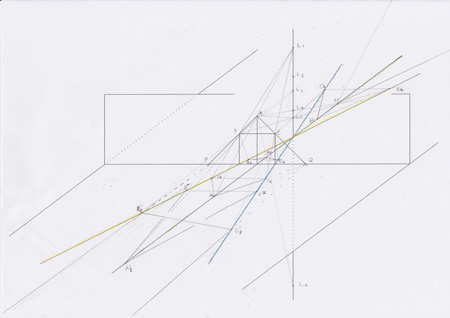
光源と、壁に三角形の穴が空いている場合、その影はどのようになるか?光源が上の方にある場合、現実的な影でイメージしやすく作図も説明しやすい。しかし、光源が下のほうへ、さらには、地面の下とかに仮定した場合、実際的にはイメージできない。でも法則に合致している部分に書くことができる。現実的にありえないところになるが、法則的にはあっている不思議。
今回の講義の内容としては、射影幾何学の最初の一歩といったところで、まだまだ、先が相当長いそうだ。
今回の講義を聞いていて思ったのは、無限遠というもの(現実的には非常識なもの)を追加すると仮定した場合、今までの常識はそのままで、あらたに発見することがあるということだ。現状の常識を無茶苦茶にする仮定ならいざしらず、常識に影響を与えない仮定によって、新たな気づき、発見があるのかもしれない。
現状見えているものは、世界の半分しか見えていないのかも?と思った。
P.S.
この講義を受けるために、「エーテル空間」をなんとか全部読んでから受講したいと、間に合うように一生懸命読んだ。エーテル空間がイメージできるように、いやイメージできなくても、なんとなくでも今以上に自分なりに理解したいものだ。もう一度、丹羽さんの「射影幾何学入門」を再度読み直してみるかなあ(途中で読むのを挫折した)。
Tweet
Edited by たわふ 2013/02/05 16:00:13
Last Modified 2013/02/05 16:51:09